Caracterización semianalítica y numérica de agujeros negros acústicos en terminaciones de conductos

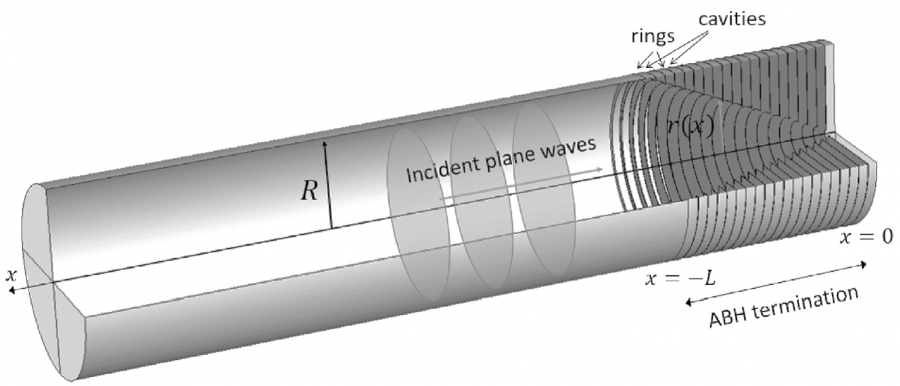
En los últimos años, se ha estudiado el efecto de los agujeros negros acústicos (ABHs) para controlar el ruido en conductos, aunque originariamente se desarrollaron para la propagación de ondas estructurales en vigas y placas. Un ABH puede caracterizarse de diferentes formas: mediante técnicas matemáticas analíticas, con el método de las matrices de transferencia (TMM) o con el método numérico de los elementos finitos (FEM), a la vez que con experimentos. En esta tesis se consideran los tres métodos citados. Se propone un nuevo marco teórico, basado en la discretización de la formulación variacional de la ecuación de Helmholtz utilizando funciones de base Gaussianas. El problema considerado incluye una superficie residual rígida en la terminación del ABH y el enfoque propuesto permite calcular los modos del ABH a partir de un problema de valores propios. Este enfoque semianalítico se ha validado con simulaciones FEM y el grado de similitud es muy notable. A continuación, se ha introducido el método de las matrices de transferencia y se ha aplicado al problema de los ABHs. Se demuestra que la solución TMM tiende formalmente a la solución de la ecuación del ABH en el caso límite en el que el número de anillos tiende a infinito. A tal efecto se utiliza el concepto de metamaterial y se discute la analogía entre una onda acústica que se propaga en un ABH y una onda que se propaga en un conducto lleno de un metafluido con propiedades físicas particulares. Por último, se obtienen y se discuten algunos resultados preliminares de los ABHs obtenidos con FEM. Se analiza la influencia de distintos parámetros, como el número de anillos y el orden del ABH en el coeficiente de reflexión del ABH. Los resultados FEM son los más costosos (con respecto al coste computacional) y los más cercanos a la realidad. De hecho, el FEM permite visualizar y entender mejor la física en el interior de la terminación ABH.