A semi-analytical method for characterizing vibrations in circular beams with embedded acoustic black holes

While acoustic black holes (ABHs) in mechanics have been primarily tested for flat surfaces, structures in the aerospace, naval and further industries involve many curved structures. In this work, a first step is carried out towards the characterization of ABHs in curved beams. In particular, the reduction of flexural waves in a circular beam with various embedded AVHs is analyzed showing the usefulness of the ABH effect. The appearance of frequency stopbands typical of periodic structures is reported.
Details on this research can be found in the paper:
Jie Deng, Oriol Guasch and Ling Zheng (2020), "A semi-analytical method for characterizing vibrations in circular beams with embedded acoustic black holes". Journal of Sound and Vibration, 476, 115307.
(https://www.sciencedirect.com/science/article/abs/pii/S0022460X20301383)
with abstract:
Acoustic black hole (ABH) indentations have proven to be an efficient way for reducing vibrations on straight beams and plates. However, many built-up structures in the naval and aerospace sectors involve curved beams and shells, so there is a need to check whether the ABH effect could be also beneficial for them. To date, such issue has not been yet addressed and in this work some initial steps are proposed towards it. In particular, an analysis is made of the vibrational behavior of a circular beam with embedded ABHs. A semi-analytical model is suggested in the framework of the Rayleigh-Ritz method, making use of Gaussian trial functions. The key to the approach is building a basis of Gaussian functions that fulfill the periodic boundary conditions on the beam, to approximate its radial and tangential motions. It is shown how this can be done quite directly and efficiently. The validity of the proposed approach is then tested by comparison with finite element simulations, showing very good matching. The Gaussian expansion is then applied to study the dependence of the bending vibration of an ABH circular beam with frequency. After that, the influence of curvature and boundary conditions are established by comparing the performance of close and open circular ABH beams and straight periodic beams. Circular beams containing different number of ABHs are also studied and the appearance of frequency stopbands is reported.
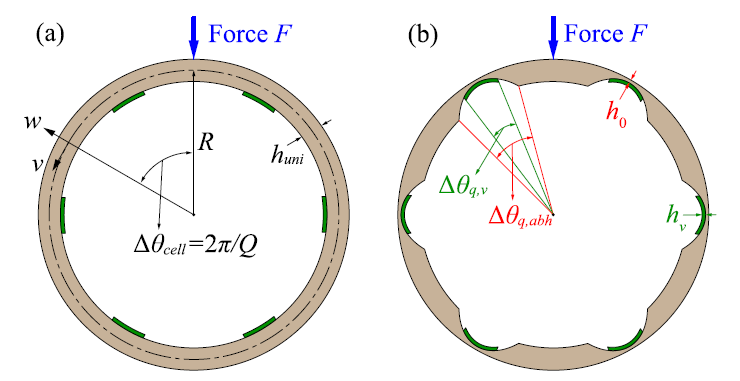
Figure. Uniform circular beam versus circular beam with embedded Acoustic Black Holes. The green layers represent viscoelastic materials to dissipate energy at the center of the ABHs.