Energy-based methods for multiple connected subsystems in vibroacoustics
The audible range covers four frequency orders of magnitude, from 20 Hz to 20000 Hz, so in vibroacoustics we need different methods to solve problems at low, mid and high frequencies. While deterministic approaches are valid for lower frequencies (e.g., the finite element method, FEM), statistical methods like the statistical energy analysis (SEA) are needed for higher frequencies. SEA allows one to simulate very large structures, e.g., an entire airplane, a building or a railway coach, at a very reasonable computational cost.
Statistical energy methods in vibroacoustics, like SEA or the statistical modal energy distribution analysis (SmEdA), rely on specific modal coupling assumptions (MCAs) between subsystem modes. These methods assume that the behavior of subsystem mode amplitudes mimic that of oscillators, that the modes within a subsystem are uncoupled, and that the coupling between two different subsystems only takes place through the interaction of resonant modes. In the case of more than two subsystems being connected at a junction, however, it becomes difficult to establish a modal interaction scheme for them. In SEA, the problem is avoided by resorting to the travelling wave approach instead of the modal one. Nevertheless, there is a need for other energy-based methods, like SmEdA, to deal with such a situation.
In a series of the two companion papers below, the authors propose two different approaches to deal with multiple flexural waveguides connected at a junction. The first one constitutes an extension of the displacement-stress dual formulation, originally intended for two subsystems, to the case of multiple ones. The method works whenever there is a strong impedance mismatch between subsystems. When that is not the case, it is shown that the situation can be addressed by means of a reformulated version of the well-known Craig-Bampton method.

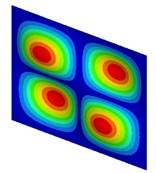
Figure. Global mode at 80.4 Hz versus local mode at 80.5 Hz for a four plate connection with strong impedance mismatch.
This research is a result from the ongoing fruitful collaboration between the Laboratoire Vibrations-Acoustique (LVA) from the INSA in Lyon, France, and the Engineering Department of La Salle, Universitat Ramon Llull.
Laurent Maxit and Oriol Guasch (2019), "A dual modal formulation for multiple flexural subsystems connected at a junction in energy-based models". Mechanical Systems and Signal Processing, 119, pp. 457-470. Link
Laurent Maxit and Oriol Guasch (2019), "Energy-based reformulated Craig-Bampton method for multiple flexural subsystems connected at a junction with low impedance mismatch". Mechanical Systems and Signal Processing, 119, pp. 471-485. Link
The second author of the papers would like to thank l'Obra Social de la Caixa and the Universitat Ramon Llull for their support under grant 2018-URL-IR2nQ-031.