Quantum Algorithms for solving Hard Constrained Optimization Problems

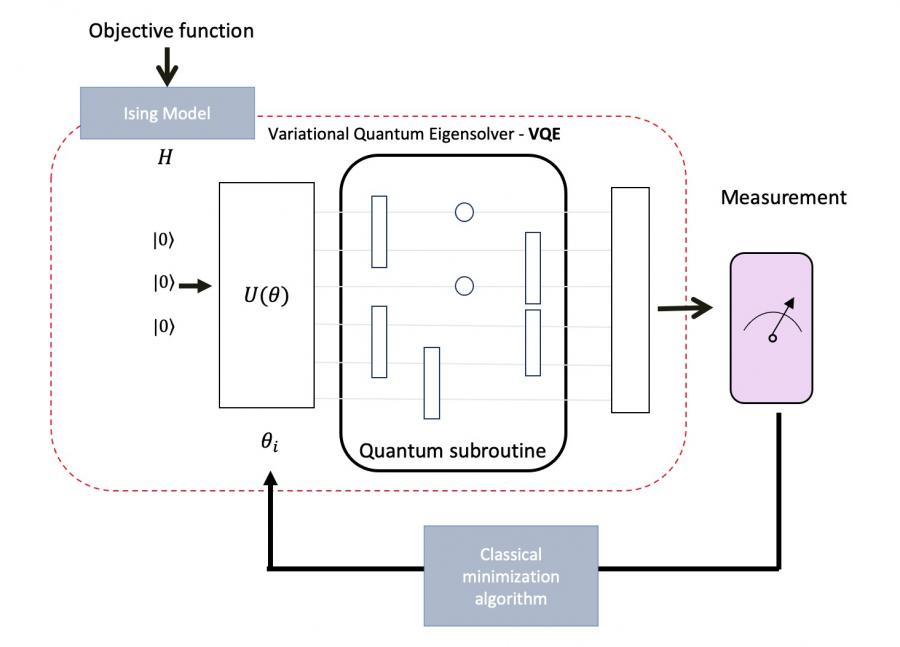
In this research, Combinatorial optimization techniques to solve constraint problems have been examined. A study of the quantum era and market leaders such as IBM, D-Wave, Google, Xanadu, AWS-Braket and Microsoft has been carried out. We have learned about their community, their platforms, the status of their research, and the postulates of quantum mechanics that create the most efficient quantum systems and algorithms. To know if it is possible to solve Constraint Search Problem (CSP) problems more efficiently with quantum computing, a scenario was defined so that both classical and quantum computing would have a good point of reference. First, the proof of concept focuses on the social worker scheduling problem and later on the issue of batch picking and order picking as a generalization of the Social Workers Problem (SWP). The social workers programming problem is a combinatorial optimization problem that can be solved exponentially at best; seeing that the SWP is NP-Hard, it claims using another approach beyond classical computation for its resolution. Today, the focus on quantum computing is no longer only on its enormous computing power but also on the use of its imperfection in this era Noisy Intermediate-Scale Quantum (NISQ) to create a powerful machine learning device that uses the variational principle to solve optimization problems by reducing their complexity class. In the thesis, a (quadratic) formulation is proposed to solve the problem of social workers' schedules efficiently using Variational Quantum Eigensolver (VQE), Quantum Approximate Optimization Algorithm (QAOA),  Minimal Eigen Optimizer and ADMM optimizer. The quantum feasibility of the algorithm has been modelled in QUBO form, with Cirq simulated, Or-Tools and tested on IBMQ computers.
After analyzing the results of the above approach, a scenario was designed to solve the SWP as quantum case-based reasoning (qCBR), both quantum and classically. And thus, to be able to contribute with a quantum algorithm focused on artificial intelligence and machine learning. The qCBR is a machine learning technique based on solving new problems that use experience, as humans do. The experience is represented as a memory of cases containing previously resolved questions and uses a synthesis technique to adapt the background to the new problem better.
In the definition of SWP, if instead of patients there are batches of orders and instead of social workers mobile robots, the objective function and the restrictions are generalized. To do this, a proof of concept and a new formulation has been proposed to solve the problems of picking and batching called qRobot. A proof of concept was carried out in this part of the project through a Raspberry Pi 4 and the integration capacity of quantum computing within mobile robotics was tested, with one of the most demanded problems in this industrial sector: picking and batching problems. It was tested on different technologies, and the results were promising. Furthermore, in case of computational need, the robot parallelizes part of the operations in hybrid computing (quantum + classical), accessing CPU and QPU distributed in a public or private cloud. Furthermore, we developed a stable environment (ARM64) inside the robot (Raspberry) to run gradient operations and other quantum algorithms on IBMQ, Amazon Braket (D-Wave) and Pennylane locally or remotely.
To improve the execution time of variational algorithms in this NISQ era and the next, EVA has been proposed: A quantum Exponential Value Approximation algorithm. To date, the VQE is the flagship of quantum computing. Today, in the market-leading quantum cloud computing platforms, the cost of experimenting with quantum circuits is proportional to the number of circuits running on those platforms. That is, with more circuits, higher cost. One of the things that the VQE, the flagship of this low-qubit era, achieves is shallow depth by dividing the Hamiltonian into a list of many small circuits (Pauli matrices). But this very fact makes simulating with VQE very expensive in the cloud. For this same reason, EVA was designed to calculate the expected value with a single circuit.
 
Even having answered the hypothesis of this work with all the studies carried out, it is still possible to continue research to propose new quantum algorithms to improve combinatorial optimization.