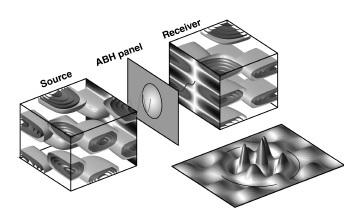
En áreas como la aeronáutica, los vehículos submarinos y el transporte civil, entre otros, reducir las vibraciones estructurales y el nivel de presión acústica supone un reto difícil. En los últimos años se ha propuesto el concepto de los agujeros negros acústicos en mecánica (conocidos por sus siglas ABH del inglés, Acoustic Black Hole) a tal efecto. Los ABHs han atraído la atención de la comunidad de investigación en vibroacústica y suelen estar formados por muescas en vigas y placas, cuyo grosor decae según una ley potencial. El efecto del ABH es el de ralentizar las velocidades de fase y de grupo de las ondas de flexión incidentes de tal modo que, en teoría, haría falta un tiempo infinito para que las ondas alcanzaran el centro del ABH, si el grueso de este último fuera exactamente cero. Sin embargo, en la práctica esto no es posible, aunque se puede conseguir una fuerte disipación colocando una capa de material amortiguador en el centro del ABH, donde se concentra la mayor parte de la energía de las ondas. En los últimos años, los ABHs no sólo se han explotado como método pasivo para reducir vibraciones estructurales y la consecuente emisión de ruido, sino que también se ha explorado su potencial para otras aplicaciones como la manipulación de ondas o la captación de energía.
Esta tesis tiene tres objetivos principales. Así pues, tras una introducción general a los ABHs, el trabajo se ha dividido en tres grandes secciones. La primera aborda aplica- ciones de los ABHs en vigas rectas y placas planas. Para empezar, se propone y analiza un voladizo piezoeléctrico con un acabado de ABH para capturar energía que que evita el problema de la disminución de la longitud de onda en el extremo del ABH. A continuación, se presentan ABHs en forma de anillo para aislar puntos de excitación externos en placas planas y así evitar la transmisión de vibraciones. Finalmente, se contemplan configuraciones periódicas de matrices de ABHs para colimar haces de ondas de flex- ión y concentrar su energía en zonas predeterminadas de una placa. La segunda parte de la tesis propone nuevos diseños de ABHs para estructuras con curvatura. Estas son muy habituales en los sectores naval, aeronáutico e industrial, por lo que merece la pena investigar si los ABH pueden dar buenos resultados en algunos casos. La sec- ción comienza analizando la inclusión de ABHs en vigas circulares y se ve como estos dan pie a la aparición de fenómenos típicos de sistemas periódicos. Seguidamente se propone un ABH anular para reducir las vibraciones en conductos cilíndricos. En con- creto, se tratan los casos de un conducto simplemente soportado con un ABH anular, y el de un conducto con ABH, soportes periódicos y rigidificadores. Se presta especial atención a algunos resultados inesperados. Para finalizar la sección, se investigan los efectos de los ABH anulares en la radiación acústica del conducto teniendo en cuenta el nivel de potencia acústica, la eficiencia de radiación y la intensidad supersónica, y se observa una mejora notable respecto a los conductos cilíndricos de espesor uniforme. La tercera parte de la tesis es más corta que las anteriores y simula el aislamiento de una placa con múltiples ABHs, en el rango de media y alta frecuencia. A tal efecto se emplea el método del análisis estadístico de distribución modal de energía (SmEdA: statistical modal energy distribution analysis). En esta sección, la estructura con ABHs ya no se analiza como un elemento individual, sino que se acopla a dos cavidades de aire formando parte de un sistema mecánico más complejo.
A lo largo de la tesis se utiliza repetidamente el método de expansión gaussiana (GEM: Gaussian expansión method). Por GEM entendemos tomar funciones gaus- sianas como base para resolver ecuaciones diferenciales en derivadas parciales en el marco del método de Rayleigh-Ritz. El GEM se parece mucho a los enfoques de ondícu- las, pero ofrece algunas ventajas en el caso de condiciones de contorno periódicas. Al principio de la tesis se expone un breve repaso del GEM y, cuando es necesario, se aborda su reformulación para un problema particular en el capítulo correspondiente.