Acoustic black hole in duct termination as a realization of a metafluid.

Acoustic black holes (ABHs) have revealed as a new and original approach to achieve anechoic terminations in ducts and inspire future muffler designs. The performance of ABHs can be characterized by means of the transfer matrix method (TMM), yet to date there was no mathematical proof of its consistency. Researchers from the GTM Prof. Oriol Guasch, Dr. Patricia Sánchez-Martín and Davide Ghilardi have recently filled this gap. They have shown that an ABH termination made of duct rings with decreasing inner radii can be viewed as a practical realization of a metafluid of increasing density (see figure below). A metafluid (metamaterial) can be understood as a fluid (material) with on-demand effective properties and without the constraints imposed by what nature provides. Applying the TMM to the metafluid allows one to prove that the method is mathematically consistent and that the TMM solution tends to that of the ABH continuous equation.
Details on this research can be found in the paper:
Oriol Guasch, Patricia Sánchez-Martín and Davide Ghilardi (2020), "Application of the transfer matrix approximation for wave propagation in a metafluid representing an acoustic black hole duct termination". Applied Mathematical Modelling, 77 (2), pp. 1881-1893. (https://www.sciencedirect.com/science/article/abs/pii/S0307904X19305700)
with abstract:
The transfer matrix method has been proposed to analyze the acoustic black hole effect in duct terminations. The latter is achieved by placing a retarding waveguide structure inside the duct, which consists in a set of rings whose inner radii decrease to zero following a power law. The rings are separated by thin air cavities. If the number of ring-cavity ensembles is large enough, wave propagation inside the waveguide can be treated as a continuous problem. A governing differential equation can be derived for the acoustic black hole which intrinsically relies on assumptions from transfer matrix theory. However, no formal demonstration exists showing that the transfer matrix solution is consistent and formally tends to the solution of the continuous problem. Proving such consistency is the main goal of the paper and an original option has been adopted to this purpose. First, we prove the differential equation for the acoustic black hole is identical to the wave equation for a metafluid with a power-law varying density. Transfer matrices are then applied to solve wave propagation in a discretization of the metafluid into layers of constant density. We then show that when the number of layers tends to infinity and their thicknesses to zero, the transfer matrix solution satisfies the metafluid equation and therefore the acoustic black hole one. The transfer matrices for the metafluid discrete layers take a particularly simple form, which is a great advantage. This work allows one to interpret the retarding waveguide structure as a particular realization of the metafluid.
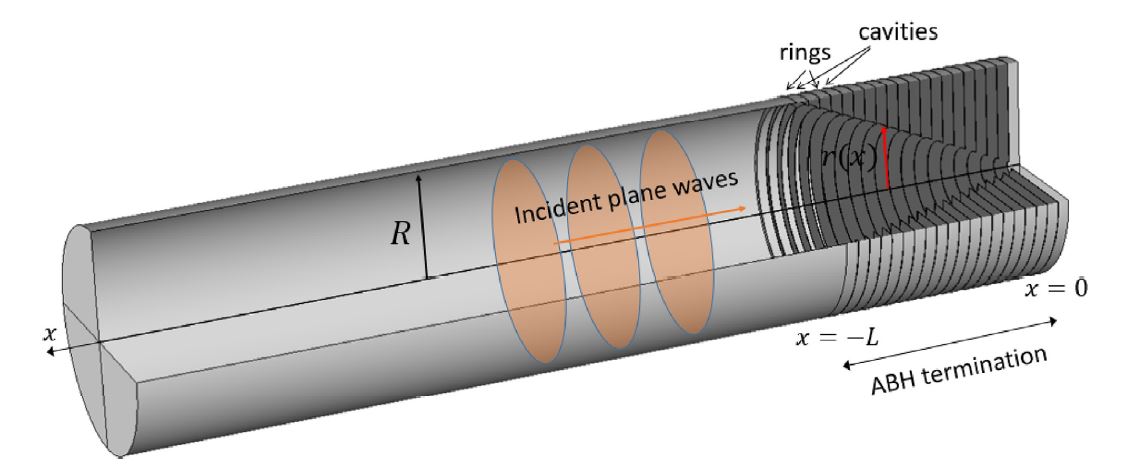
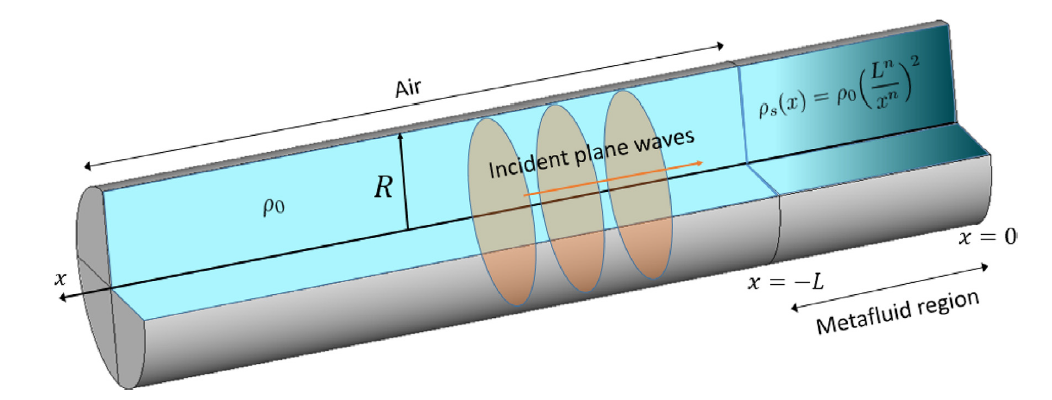
Figure. The acoustic black hole (ABH) in a duct termination is made of a set of concentric rings with power-law decreasing radius (top image). The ABH can be interpreted as a realization of a metafluid with power-law varying density (bottom image).